Attention
注意力机制(Attention Mechanism)的提出为了解决 seq2seq 在长序列中的遗忘问题(状态向量无法记住所有信息)。由 Dzmitry Bahdanau 于 ICLR 2015 年在《Neural Machine Translation by Jointly Learning to Align and Translate》论文中提出。
本文是我学 Shusen Wang 老师课程视频的笔记,笔记中很多图片来自于课程的截图,在此统一注明出处。
核心思想:Decoder 每次更新状态的时候,都会再看一遍 Encoder 所有状态,从而避免遗忘。Attention 还能告诉 Decoder,应该关注 Encoder 哪个状态,Attention 名称的由来。
Attention 缺点:计算量大。
自引入以来,注意力机制已经在许多深度学习任务中取得了显著的成果,如机器翻译、文本摘要、语音识别和图像描述生成等。最著名的注意力模型之一是Transformer 模型,该模型完全基于多头自注意力,无需使用传统的循环神经网络(RNN)或卷积神经网络(CNN)结构。Transformer模型是许多当今最先进的NLP模型(如BERT、GPT等)的基础。
编码阶段
编码过程与 seq2seq 是一样的,不同之处在于:seq2seq 是将最后一个隐藏状态传入解码器,而这里,是将所有隐藏状态(隐藏状态集合)共同传入解码器。
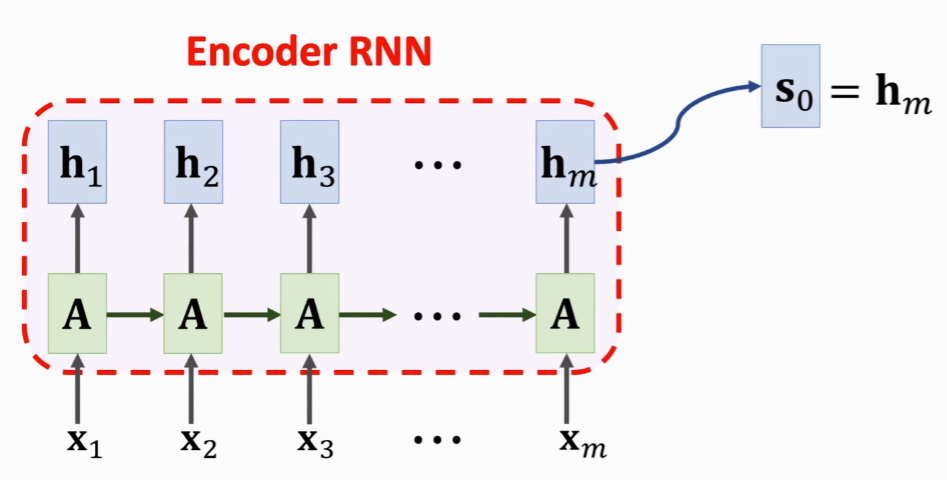
Encoder 结束工作之后,Attention 和 Decoder 同时开始工作。
解码阶段
Decoder 的初始状态
除此之外,Decoder 还需要使用一系列权重值:
- Encoder 的所有隐藏状态
,保留下来,用于计算一个相关性: - 其中
是 Encoder 第 个状态 是 Decoder 当前状态。 被称为权重,因为 Encoder 有 m 个状态,所以权重有 m 个 ,所有权重之和为1。
- 关于权重的计算方法,参见后面小节。
根据权重,可以计算上下文向量(Context Vector):
注意,
每个 Context Vector 都会对应一个 Decoder 状态
解码器输入
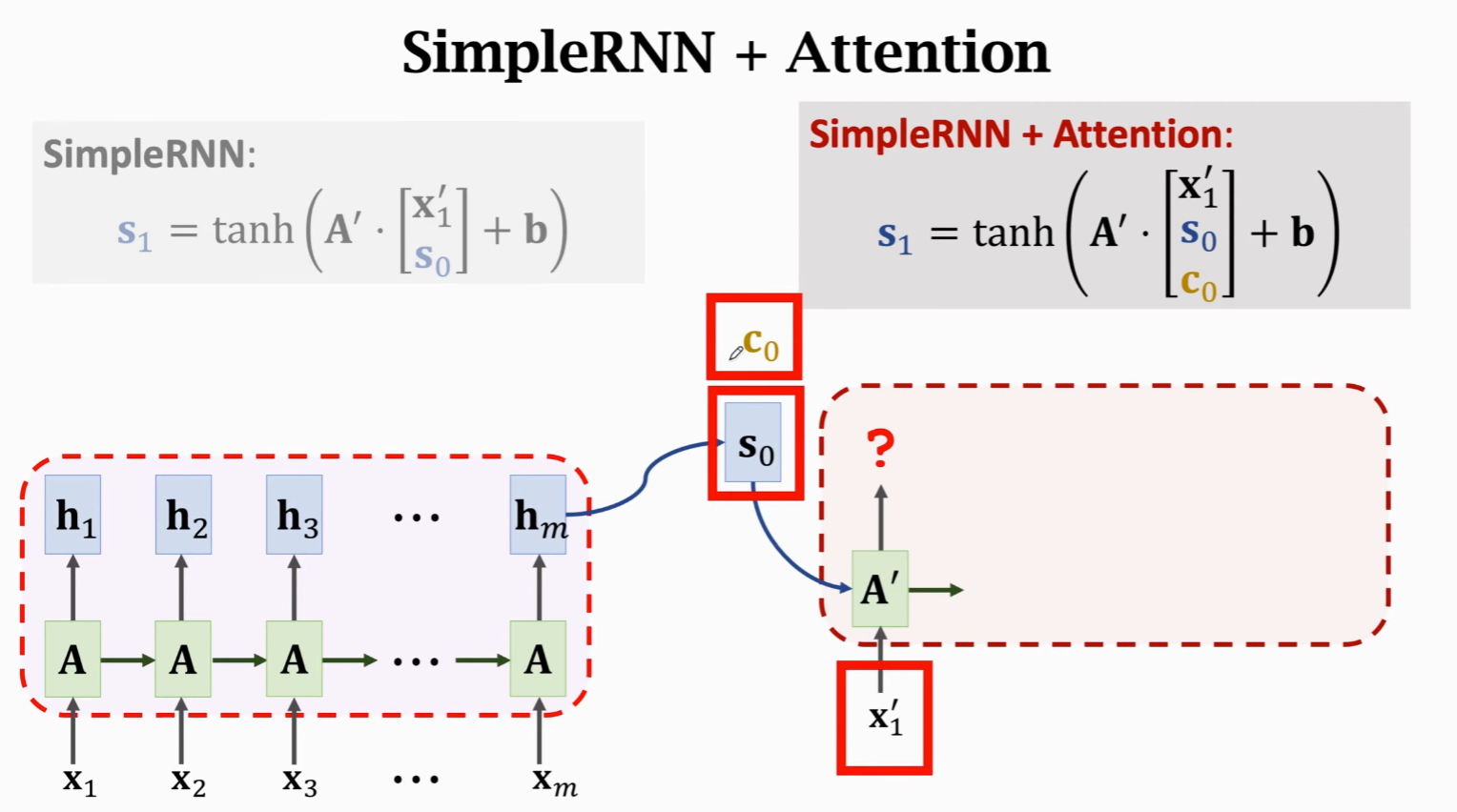
纯 RNN 的解码器输入,就是新输入
有了 Attention 后,需要拼接 Context Vector,来计算新状态。
Context Vector 是 Encoder 所有状态
因为
下一状态计算
权重计算式:
再计算 Context Vector:
Decoder 接受新输入
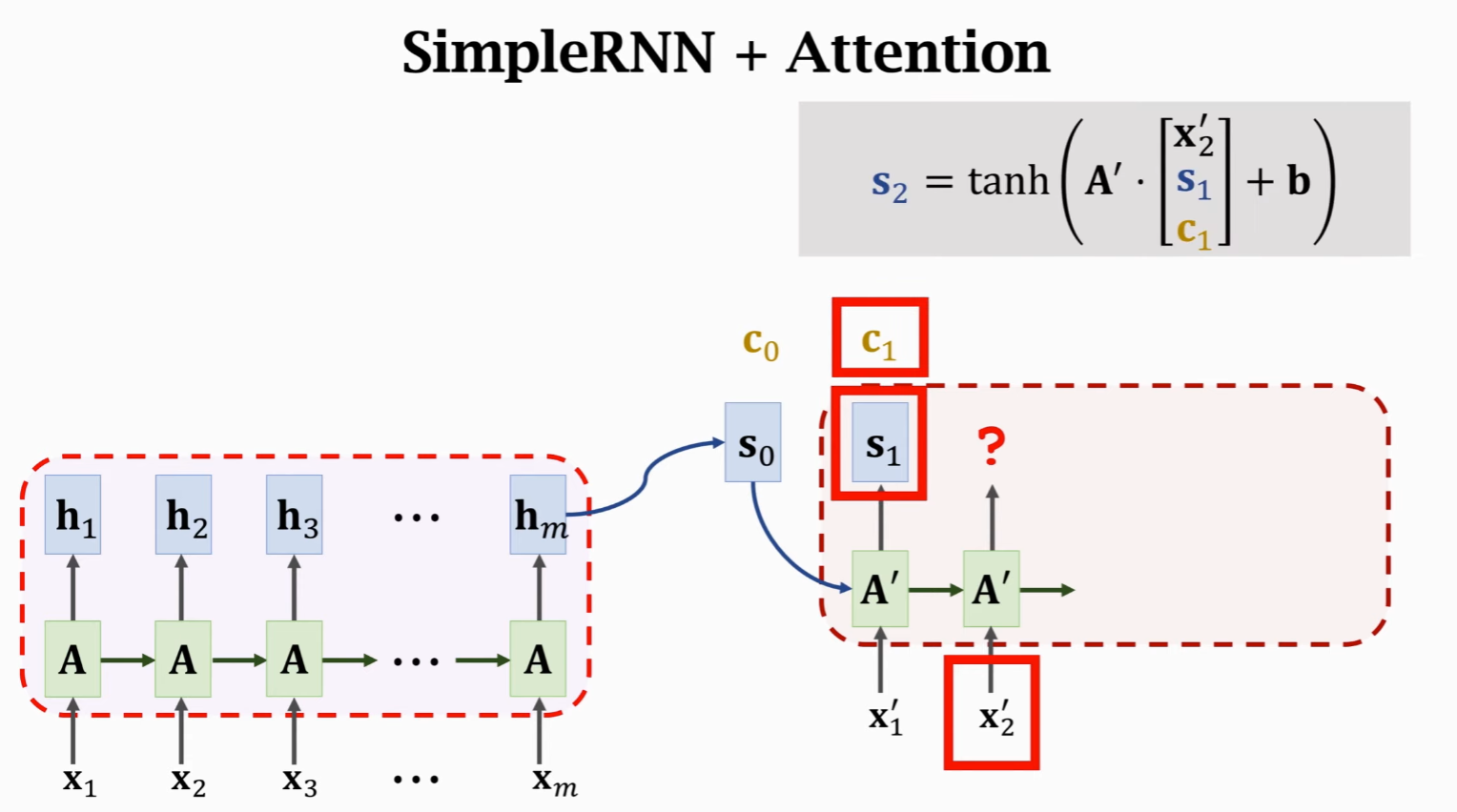
循环
如此循环往复:
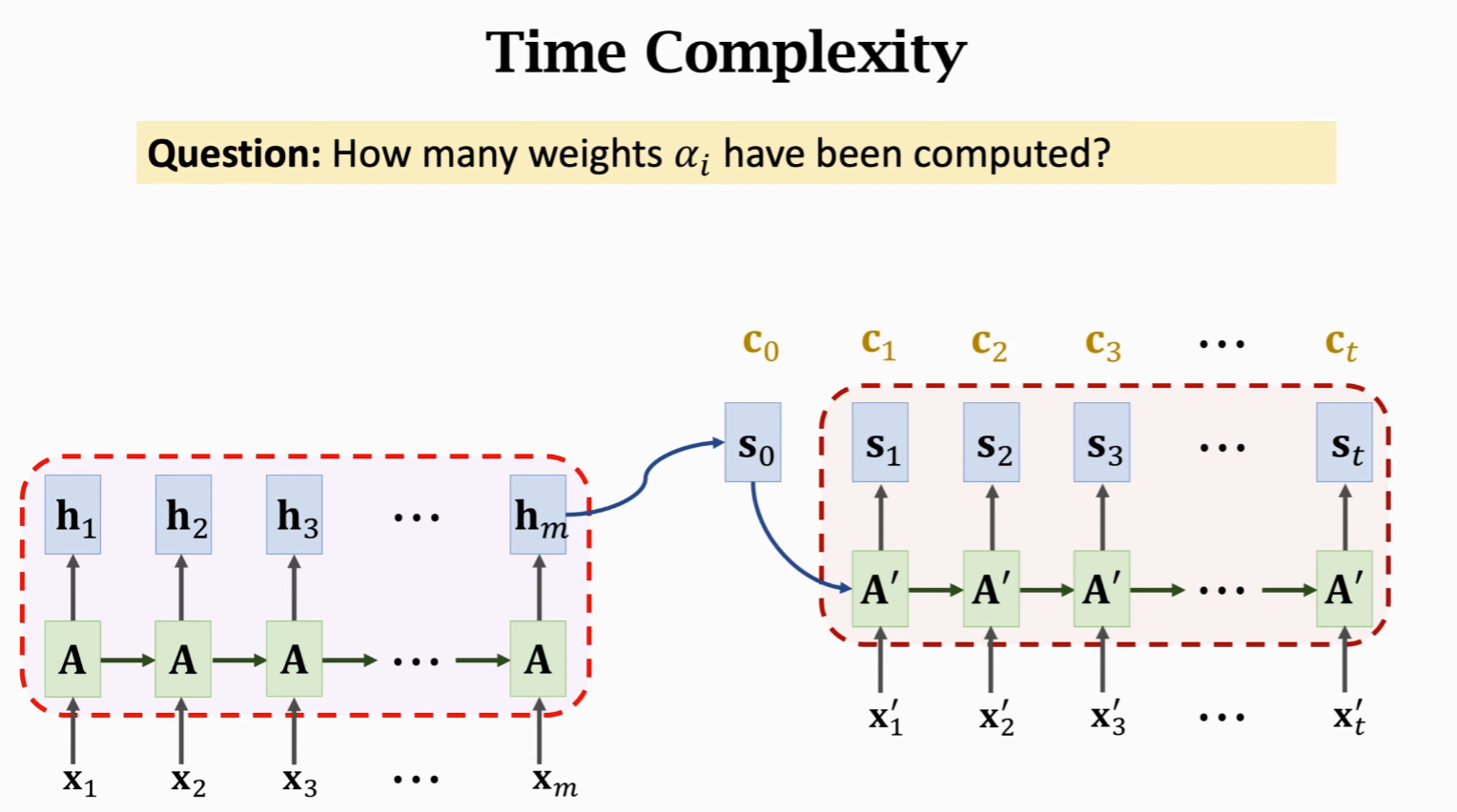
问题回答:
- 为了计算 Context Vector,需要计算 m 个权重
- 每次状态更新都要重新计算,假设有 t 个状态
- 时间复杂度为 mt(要计算 mt 此权重)
- 时间复杂度很高
直观理解权重含义
神经机器翻译,Encoder 在下,Decoder 在上。
Attention 会把 Decoder 的每个状态与 Encoder 每个状态作对比,得到两者相关性(即权重
线表示 Decoder 状态与 Encoder 状态的关联,粗的线表示权重大,细的表示权重小。两个状态的相关性高。
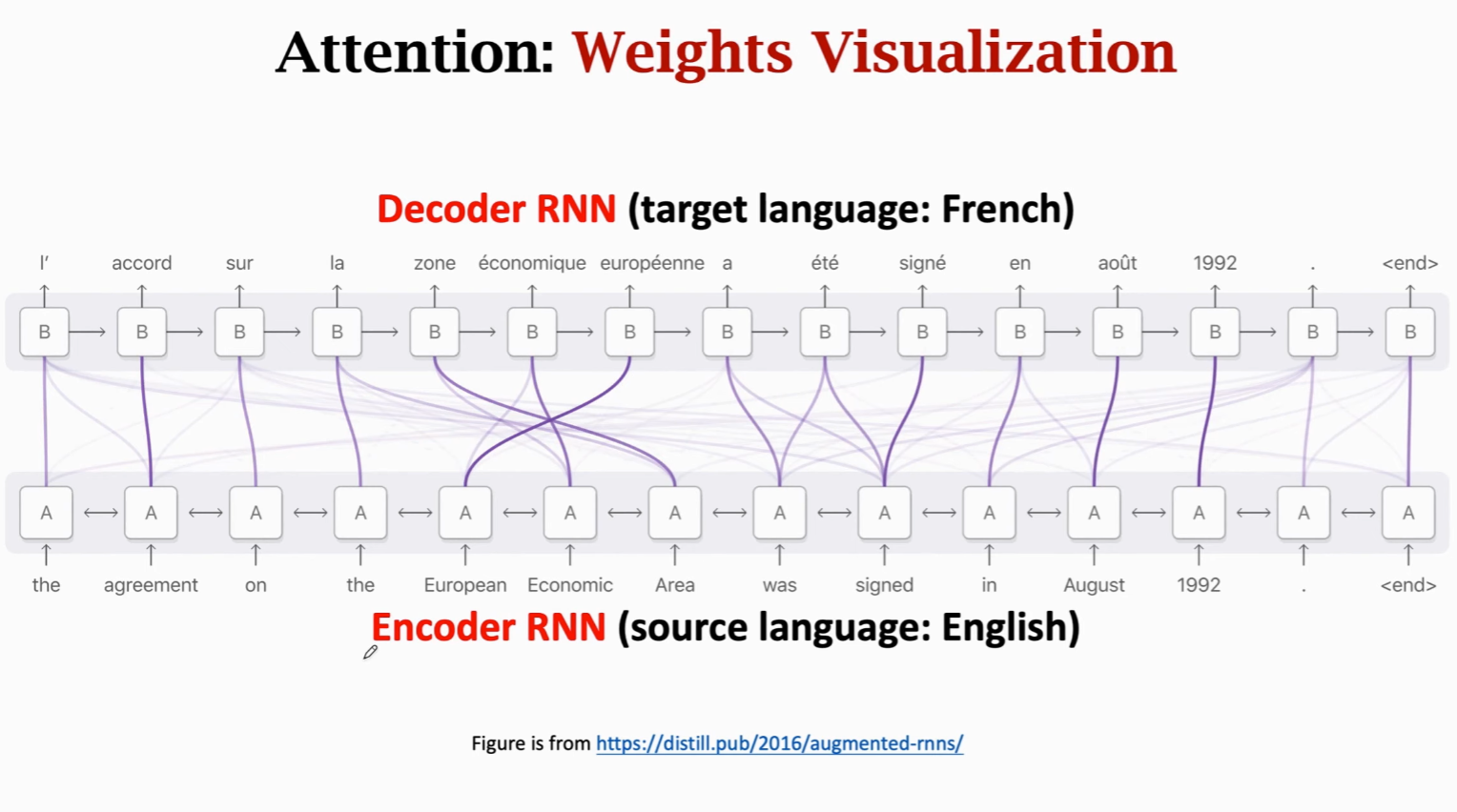
每当 Decoder 想要生成一个状态的时候,都会看一遍 Encoder 所有的状态。权重告诉 Decoder 该关注什么地方——Attention 名字的由来。
帮助 Decoder 生成正确的状态,从而生成正确的输出。
如何计算权重
原始论文方法
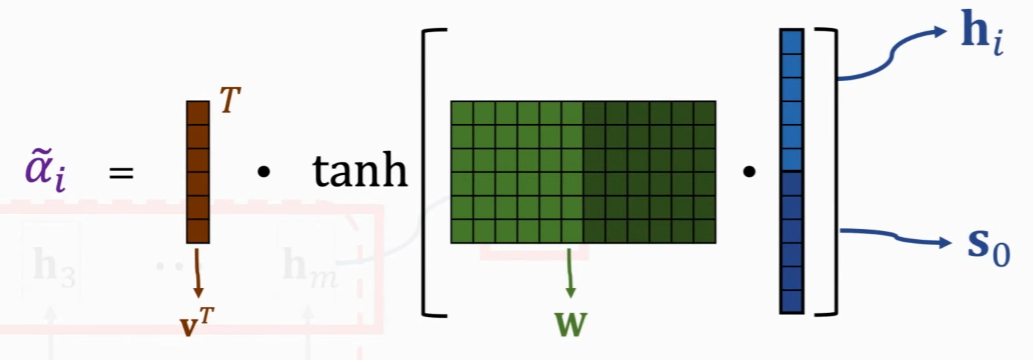
将
再计算向量 v 与刚刚算出来向量的内积,得到
v 和
之后进行 normalize(相加之和为 1):
这是原始论文中提出的方法,在此之后,有很多其他论文提出权重计算方法。
Transformer 方法
更加流行的方式。输入还是
两个 W 参数矩阵,需要从训练数据中学习。
计算两个向量内积:
之后进行 normalize(相加之和为 1):
网络资源
- RNN模型与NLP应用(8 of 9):Attention (注意力机制):https://www.youtube.com/watch?v=XhWdv7ghmQQ
- Seq2Seq With Attention - 知乎
- Seq2Seq模型和Attention机制 - machine-learning-notes
本文作者:Maeiee
本文链接:Attention
版权声明:如无特别声明,本文即为原创文章,版权归 Maeiee 所有,未经允许不得转载!
喜欢我文章的朋友请随缘打赏,鼓励我创作更多更好的作品!
