PyTorch 神经网络分类器
根据文本的词袋模型来对文本进行建模,然后利用一个神经网络来对文本进行分类。
使用带有标签的商品评论信息训练神经网络。
本实例来自《深度学习原理与PyTorch实战(第2版)》,本文是我对该节的自学实践。
Softmax 函数
分类问题的损失函数
如何对分类网络定义损失函数?通常采用交叉熵(Cross-Entropy)形式的损失函数。
通俗理解交叉熵
交叉熵其实就是在衡量我们的预测和真实情况之间的差距。
假设你有一张考卷,上面有10道题,每题10分,老师告诉你每道题的正确答案。那么这个正确答案就是"真实情况"。而你自己作答的结果,就是你的"预测"。
如果你答对了一道题,就得10分。如果答错了,就得0分。那么你的总分就反映了你的预测和正确答案之间的差距。如果你得了100分,说明你的预测完全正确。如果你只得了50分,说明你的预测和真实情况差距很大。
交叉熵就像这个总分一样,它衡量了我们的预测分布和真实分布之间的差异。如果交叉熵的值很小,就像你的总分很高一样,说明我们的预测和真实情况很接近。如果交叉熵的值很大,就像你的总分很低一样,说明我们的预测和真实情况差得很远。
在机器学习中,我们希望机器能尽量准确地预测结果。所以我们希望交叉熵的值尽可能小,就像你希望考试的分数尽可能高一样。这就是为什么在训练机器学习模型的时候,我们要尽量去最小化交叉熵的值。
那么机器是如何计算交叉熵的呢?它会看每一个可能的类别,比较模型预测的概率和真实情况下这个类别的概率,然后把所有类别的差异加起来。这就像是把每道题的得分加起来算总分一样。
我们之所以用交叉熵,是因为它特别"严格"。如果模型在某个类别上预测错了,而这个类别恰好是正确答案,那交叉熵会给予很大的惩罚,就像老师会对那些简单问题答错的学生扣更多的分一样。这就促使我们的模型更加努力地去学习,尽量避免犯这样的错误。
词袋模型分类器
词袋(Bag of Words)模型是一种简单而有效的对文本进行向量化表示的方法。早在1954年,美国著名语言学家泽里格·哈里斯(Zellig Harris)就提出了这个模型。
简单来讲,词袋模型就是将一句话中的所有单词都放进一个袋子(单词表)里,而忽略语法、语义,甚至单词之间的顺序等信息。
先对中文进行分词,不考虑顺序,将这些词建立一个词典(形成一个大向量空间),然后每个自言语言句子,根据词频,变成这个大向量空间上的点。
导入包
# 导入程序所需要的程序包
#抓取网页内容用的程序包
import json
import requests
#PyTorch用的包
import torch
import torch.nn as nn
import torch.optim
#from torch.autograd import Variable
# 自然语言处理相关的包
import re #正则表达式的包
import jieba #结巴分词包
from collections import Counter #搜集器,可以让统计词频更简单
#绘图、计算用的程序包
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
语料准备
本例中使用的语料位于这里。
- 正面数据:
good.txt - 负面数据:
bad.txt
使用 jieba 进行分词。具体数据处理代码如下:
# 数据来源文件
good_file = 'good.txt'
bad_file = 'bad.txt'
# 将文本中的标点符号过滤掉
def filter_punc(sentence):
sentence = re.sub("[\s+\.\!\/_,$%^*(+\"\'“”《》?“]+|[+——!,。?、~@#¥%……&*():]+", "", sentence)
return(sentence)
# 扫描所有的文本,分词并建立词典,分出正面还是负面的评论,is_filter可以过滤标点符号
def Prepare_data(good_file, bad_file, is_filter = True):
all_words = [] # 存储所有的单词
pos_sentences = [] # 存储正面评论
neg_sentences = [] # 存储负面评论
with open(good_file, 'r', encoding='utf-8') as fr:
for idx, line in enumerate(fr):
if is_filter:
# 过滤标点符号
line = filter_punc(line)
# 分词
words = jieba.lcut(line)
if len(words) > 0:
all_words += words
pos_sentences.append(words)
print('{0} 包含 {1} 行,{2} 个单词.'.format(good_file, idx+1, len(all_words)))
count = len(all_words)
with open(bad_file, 'r', encoding='utf-8') as fr:
for idx, line in enumerate(fr):
if is_filter:
line = filter_punc(line)
words = jieba.lcut(line)
if len(words) > 0:
all_words += words
neg_sentences.append(words)
print('{0} 包含 {1} 行,{2} 个单词.'.format(bad_file, idx+1, len(all_words)-count))
# 建立词典,diction的每一项为{w:[id, 单词出现次数]}
diction = {}
cnt = Counter(all_words)
for word, freq in cnt.items():
diction[word] = [len(diction), freq]
print('字典大小:{}'.format(len(diction)))
return(pos_sentences, neg_sentences, diction)
# 调用Prepare_data,完成数据处理工作
pos_sentences, neg_sentences, diction = Prepare_data(good_file, bad_file, True)
st = sorted([(v[1], w) for w, v in diction.items()])
还写了两个方便的工具函数:
#根据单词返还单词的编码
def word2index(word, diction):
if word in diction:
value = diction[word][0]
else:
value = -1
return(value)
#根据编码获得单词
def index2word(index, diction):
for w,v in diction.items():
if v[0] == index:
return(w)
return(None)
模型
分词后可建立一个 7133 个词的词典。
使用一个 3 层神经网络,第一层 7133 各输入节点,第二层 10 个节点,输出层 2 个节点,分别表示好和差。
这个模型主要是训练分析有正面意义和负面意义的词。
文本数据向量化
使用词袋模型将文本数据向量化。将数据集分为 3 部分:
- 训练集
- 校验集:用于验证模型是否产生过拟合
- 测试集
比例是 10:1:1。训练方法:
首先,在训练模型的时候,是不使用校验集的。其次,在一组超参数下,当我们训练好模型之后,可以利用校验集的数据来测试模型的表现,如果误差与训练数据同样低或差不多,就说明模型的泛化能力很强,否则就说明出现了过拟合的现象。
为什么不能用测试集作为校验集?
这是因为当我们刻意调节超参数,使模型在校验集上有突出表现的时候,可能会导致模型加调试员这个人机系统在训练集加校验集这个整体上过拟合。
# 输入一个句子和相应的词典,得到这个句子的向量化表示
# 向量的尺寸为词典中词汇的个数,i位置上面的数值为第i个单词在sentence中出现的频率
def sentence2vec(sentence, dictionary):
vector = np.zeros(len(dictionary))
for l in sentence:
vector[l] += 1
return(1.0 * vector / len(sentence))
# 遍历所有句子,将每一个词映射成编码
dataset = [] #数据集
labels = [] #标签
sentences = [] #原始句子,调试用
# 处理正向评论
for sentence in pos_sentences:
new_sentence = []
for l in sentence:
if l in diction:
new_sentence.append(word2index(l, diction))
dataset.append(sentence2vec(new_sentence, diction))
labels.append(0) #正标签为0
sentences.append(sentence)
# 处理负向评论
for sentence in neg_sentences:
new_sentence = []
for l in sentence:
if l in diction:
new_sentence.append(word2index(l, diction))
dataset.append(sentence2vec(new_sentence, diction))
labels.append(1) #负标签为1
sentences.append(sentence)
#打乱所有的数据顺序,形成数据集
# indices为所有数据下标的一个全排列
indices = np.random.permutation(len(dataset))
#重新根据打乱的下标生成数据集dataset,标签集labels,以及对应的原始句子sentences
dataset = [dataset[i] for i in indices]
labels = [labels[i] for i in indices]
sentences = [sentences[i] for i in indices]
#对整个数据集进行划分,分为:训练集、校准集和测试集,其中校准和测试集合的长度都是整个数据集的10分之一
test_size = len(dataset) // 10
train_data = dataset[2 * test_size :]
train_label = labels[2 * test_size :]
valid_data = dataset[: test_size]
valid_label = labels[: test_size]
test_data = dataset[test_size : 2 * test_size]
test_label = labels[test_size : 2 * test_size]
建立神经网络
# 一个简单的前馈神经网络,三层,第一层线性层,加一个非线性ReLU,第二层线性层,中间有10个隐含层神经元
# 输入维度为词典的大小:每一段评论的词袋模型
model = nn.Sequential(
nn.Linear(len(diction), 10),
nn.ReLU(),
nn.Linear(10, 2),
nn.LogSoftmax(dim=1),
)
这里使用了 ReLU 激活函数。
定义一个计算准确率的函数:
def rightness(predictions, labels):
"""计算预测错误率的函数,其中predictions是模型给出的一组预测结果,batch_size行num_classes列的矩阵,labels是数据之中的正确答案"""
pred = torch.max(predictions.data, 1)[1] # 对于任意一行(一个样本)的输出值的第1个维度,求最大,得到每一行的最大元素的下标
rights = pred.eq(labels.data.view_as(pred)).sum() #将下标与labels中包含的类别进行比较,并累计得到比较正确的数量
return rights, len(labels) #返回正确的数量和这一次一共比较了多少元素
训练
# 损失函数为交叉熵
cost = torch.nn.NLLLoss()
# 优化算法为Adam,可以自动调节学习率
optimizer = torch.optim.Adam(model.parameters(), lr = 0.01)
records = []
#循环10个Epoch
losses = []
for epoch in range(10):
for i, data in enumerate(zip(train_data, train_label)):
x, y = data
# 需要将输入的数据进行适当的变形,主要是要多出一个batch_size的维度,也即第一个为1的维度
x = torch.tensor(x, requires_grad = True, dtype = torch.float).view(1,-1)
# x的尺寸:batch_size=1, len_dictionary
# 标签也要加一层外衣以变成1*1的张量
y = torch.tensor(np.array([y]), dtype = torch.long)
# y的尺寸:batch_size=1, 1
# 清空梯度
optimizer.zero_grad()
# 模型预测
predict = model(x)
# 计算损失函数
loss = cost(predict, y)
# 将损失函数数值加入到列表中
losses.append(loss.data.numpy())
# 开始进行梯度反传
loss.backward()
# 开始对参数进行一步优化
optimizer.step()
# 每隔3000步,跑一下校验数据集的数据,输出临时结果
if i % 3000 == 0:
val_losses = []
rights = []
# 在所有校验数据集上实验
for j, val in enumerate(zip(valid_data, valid_label)):
x, y = val
x = torch.tensor(x, requires_grad = True, dtype = torch.float).view(1,-1)
y = torch.tensor(np.array([y]), dtype = torch.long)
predict = model(x)
# 调用rightness函数计算准确度
right = rightness(predict, y)
rights.append(right)
loss = cost(predict, y)
val_losses.append(loss.data.numpy())
# 将校验集合上面的平均准确度计算出来
right_ratio = 1.0 * np.sum([i[0] for i in rights]) / np.sum([i[1] for i in rights])
print('第{}轮,训练损失:{:.2f}, 校验损失:{:.2f}, 校验准确率: {:.2f}'.format(epoch, np.mean(losses),
np.mean(val_losses), right_ratio))
records.append([np.mean(losses), np.mean(val_losses), right_ratio])
训练过程:
第0轮,训练损失:0.56, 校验损失:0.67, 校验准确率: 0.63
第0轮,训练损失:0.35, 校验损失:0.35, 校验准确率: 0.88
第0轮,训练损失:0.33, 校验损失:0.30, 校验准确率: 0.90
第0轮,训练损失:0.31, 校验损失:0.32, 校验准确率: 0.91
第1轮,训练损失:0.31, 校验损失:0.30, 校验准确率: 0.91
第1轮,训练损失:0.29, 校验损失:0.31, 校验准确率: 0.91
第1轮,训练损失:0.28, 校验损失:0.30, 校验准确率: 0.91
第1轮,训练损失:0.27, 校验损失:0.33, 校验准确率: 0.91
第2轮,训练损失:0.27, 校验损失:0.30, 校验准确率: 0.91
第2轮,训练损失:0.26, 校验损失:0.32, 校验准确率: 0.90
第2轮,训练损失:0.26, 校验损失:0.30, 校验准确率: 0.91
第2轮,训练损失:0.25, 校验损失:0.36, 校验准确率: 0.91
第3轮,训练损失:0.25, 校验损失:0.30, 校验准确率: 0.91
第3轮,训练损失:0.25, 校验损失:0.33, 校验准确率: 0.90
第3轮,训练损失:0.24, 校验损失:0.31, 校验准确率: 0.91
第3轮,训练损失:0.24, 校验损失:0.37, 校验准确率: 0.90
第4轮,训练损失:0.24, 校验损失:0.30, 校验准确率: 0.91
第4轮,训练损失:0.23, 校验损失:0.34, 校验准确率: 0.90
第4轮,训练损失:0.23, 校验损失:0.31, 校验准确率: 0.91
第4轮,训练损失:0.23, 校验损失:0.37, 校验准确率: 0.90
第5轮,训练损失:0.23, 校验损失:0.31, 校验准确率: 0.91
第5轮,训练损失:0.23, 校验损失:0.35, 校验准确率: 0.91
第5轮,训练损失:0.22, 校验损失:0.32, 校验准确率: 0.91
第5轮,训练损失:0.22, 校验损失:0.38, 校验准确率: 0.90
第6轮,训练损失:0.22, 校验损失:0.32, 校验准确率: 0.91
第6轮,训练损失:0.22, 校验损失:0.36, 校验准确率: 0.91
第6轮,训练损失:0.22, 校验损失:0.34, 校验准确率: 0.91
第6轮,训练损失:0.21, 校验损失:0.39, 校验准确率: 0.90
第7轮,训练损失:0.21, 校验损失:0.33, 校验准确率: 0.90
第7轮,训练损失:0.21, 校验损失:0.37, 校验准确率: 0.91
第7轮,训练损失:0.21, 校验损失:0.33, 校验准确率: 0.91
第7轮,训练损失:0.21, 校验损失:0.40, 校验准确率: 0.90
第8轮,训练损失:0.21, 校验损失:0.34, 校验准确率: 0.90
第8轮,训练损失:0.21, 校验损失:0.38, 校验准确率: 0.90
第8轮,训练损失:0.21, 校验损失:0.34, 校验准确率: 0.91
第8轮,训练损失:0.21, 校验损失:0.40, 校验准确率: 0.90
第9轮,训练损失:0.20, 校验损失:0.35, 校验准确率: 0.90
第9轮,训练损失:0.20, 校验损失:0.39, 校验准确率: 0.90
第9轮,训练损失:0.20, 校验损失:0.34, 校验准确率: 0.91
第9轮,训练损失:0.20, 校验损失:0.41, 校验准确率: 0.90
绘制误差曲线:
# 绘制误差曲线
a = [i[0] for i in records]
b = [i[1] for i in records]
c = [i[2] for i in records]
plt.plot(a, label = 'Train Loss')
plt.plot(b, label = 'Valid Loss')
plt.plot(c, label = 'Valid Accuracy')
plt.xlabel('Steps')
plt.ylabel('Loss & Accuracy')
plt.legend()
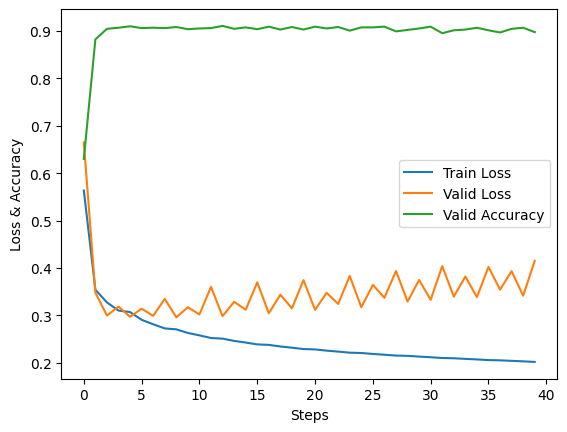
我的图跟书上不一样,书上的是未出现过拟合的情况。我这里的图,是典型的出现过拟合的情况。
大约从第 5 步之后,我就过拟合了,233333。
预测准确率
#在测试集上分批运行,并计算总的正确率
vals = [] #记录准确率所用列表
#对测试数据集进行循环
for data, target in zip(test_data, test_label):
data, target = torch.tensor(data, dtype = torch.float).view(1,-1), torch.tensor(np.array([target]), dtype = torch.long)
output = model(data) #将特征数据喂入网络,得到分类的输出
val = rightness(output, target) #获得正确样本数以及总样本数
vals.append(val) #记录结果
#计算准确率
rights = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
right_rate = 1.0 * rights[0].data.numpy() / rights[1]
right_rate
结果 0.8902532617037605
还行,书上是 90%,我这里过拟合了,也还达到了 89%。
本文作者:Maeiee
本文链接:PyTorch 神经网络分类器
版权声明:如无特别声明,本文即为原创文章,版权归 Maeiee 所有,未经允许不得转载!
喜欢我文章的朋友请随缘打赏,鼓励我创作更多更好的作品!
